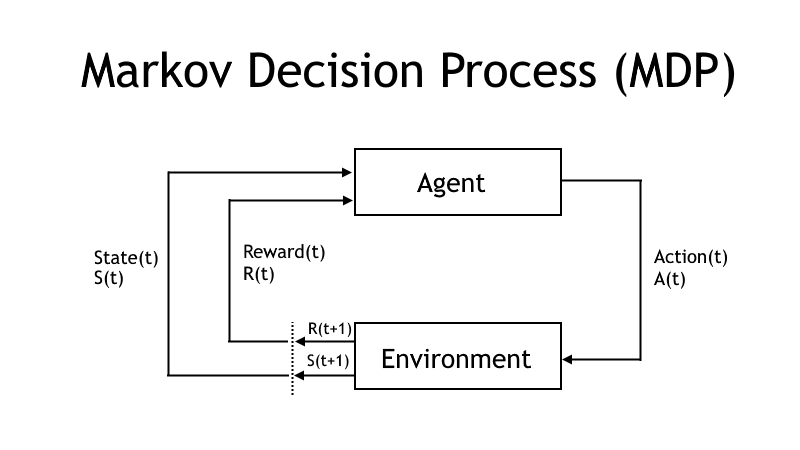
Jag kommer att tillämpa adaptiv dynamisk programmering (ADP) i denna handledning, detta för att lära en agent att gå från en punkt till ett mål över en frusen sjö. ADP är en form av passivt förstärkningslärande som kan användas i helt observerbara miljöer. Adaptiv dynamisk programmering lär sig den bästa policyn avseende en markov-beslutsprocess (MDP) som skall tillämpas på ett problem i en känd värld.
Adaptiv dynamisk programmering är en optimeringsalgoritm som lär sig den bästa policyn för åtgärder som ska utföras med hjälp av policy/värde-iteration och policyförbättringar. ADP använder sannolikhetstabeller för övergångar mellan tillstånd och nyttouppskattningar för att hitta den bästa sekvensen av åtgärder att utföra för att lösa ett problem.
ADP kommer att hitta en optimal lösning i en helt observerbar miljö. Det är dock inte möjligt att tillämpa algoritmen i stora tillståndsutrymmen, det tar alldeles för lång tid att lösa alla ekvationerna i stora tillståndsutrymmen. En diskonteringsfaktor (gamma) och ett konvergensvärde (theta) används för att hitta den bästa policyn/modellen. Theta-värdet är ett mycket litet positivt värde som indikerar om uppskattningen har konvergerat med det verkliga värdet. Diskonteringsfaktorn avgör hur viktiga framtida belöningar är, en diskonteringsfaktor på 0 betyder att aktuella belöningar är viktigast medan en diskonteringsfaktor på 1 innebär att en långsiktig belöning är viktigast.
Problem och bibliotek
En agent skall lära sig att gå från en startpunkt till en målpunkt över en frusen sjö, isen är hal och det finns hål att trilla i. Agenten belönas med 1 poäng om han når målet och 0 poäng annars, spelet är slut om agenten når målet eller om han hamnar i ett hål. Agenten kan röra sig åt vänster, neråt, åt höger eller uppåt. Rörelseriktningen är osäker på grund av det hala underlaget. Det frysta sjöproblemet är en del av gym-biblioteket, jag använder också följande bibliotek: os, random, copy, pickle, numpy and matplotlib.
Röd markör i kommandotolken
Du måste lägga till VirtualTerminalLevel och ett värde på 1 i registereditorn under HKEY_CURRENT_USER\Console om du vill att den röda markören ska visas i kommandotolken i Windows 10.
Kod
Den fullständiga koden visas nedan, den innehåller fyra olika metoder för att lösa problemet. Det är möjligt att spara och läsa in modeller med pickle. En slumpmässig policy involverar inte något lärande överhuvudtaget och visar den värsta prestationen.
# Import libraries
import os
import random
import gym
import copy
import pickle
import numpy as np
import matplotlib.pyplot as plt
# Plot values
# https://github.com/xadahiya/frozen-lake-dp-rl/blob/master/Dynamic_Programming_Solution.ipynb
def plot_values(V):
# reshape value function
V_sq = np.reshape(V, (8,8))
# plot the state-value function
fig = plt.figure(figsize=(10, 10))
ax = fig.add_subplot(111)
im = ax.imshow(V_sq, cmap='cool')
for (j,i),label in np.ndenumerate(V_sq):
ax.text(i, j, np.round(label, 5), ha='center', va='center', fontsize=12)
plt.tick_params(bottom='off', left='off', labelbottom='off', labelleft='off')
plt.title('State-Value Function')
plt.show()
# Perform a policy evaluation
# https://github.com/xadahiya/frozen-lake-dp-rl/blob/master/Dynamic_Programming_Solution.ipynb
def policy_evaluation(env, policy, gamma=1, theta=1e-8):
V = np.zeros(env.nS)
while True:
delta = 0
for s in range(env.nS):
Vs = 0
for a, action_prob in enumerate(policy[s]):
for prob, next_state, reward, done in env.P[s][a]:
Vs += action_prob * prob * (reward + gamma * V[next_state])
delta = max(delta, np.abs(V[s]-Vs))
V[s] = Vs
if delta < theta:
break
return V
# Perform policy improvement
# https://github.com/xadahiya/frozen-lake-dp-rl/blob/master/Dynamic_Programming_Solution.ipynb
def policy_improvement(env, V, gamma=1):
policy = np.zeros([env.nS, env.nA]) / env.nA
for s in range(env.nS):
q = q_from_v(env, V, s, gamma)
# OPTION 1: construct a deterministic policy
# policy[s][np.argmax(q)] = 1
# OPTION 2: construct a stochastic policy that puts equal probability on maximizing actions
best_a = np.argwhere(q==np.max(q)).flatten()
policy[s] = np.sum([np.eye(env.nA)[i] for i in best_a], axis=0)/len(best_a)
return policy
# Obtain q from V
# https://github.com/xadahiya/frozen-lake-dp-rl/blob/master/Dynamic_Programming_Solution.ipynb
def q_from_v(env, V, s, gamma=1):
q = np.zeros(env.nA)
for a in range(env.nA):
for prob, next_state, reward, done in env.P[s][a]:
q[a] += prob * (reward + gamma * V[next_state])
return q
# Perform policy iteration
# https://github.com/xadahiya/frozen-lake-dp-rl/blob/master/Dynamic_Programming_Solution.ipynb
def policy_iteration(env, gamma=1, theta=1e-8):
policy = np.ones([env.nS, env.nA]) / env.nA
while True:
V = policy_evaluation(env, policy, gamma, theta)
new_policy = policy_improvement(env, V)
# OPTION 1: stop if the policy is unchanged after an improvement step
if (new_policy == policy).all():
break;
# OPTION 2: stop if the value function estimates for successive policies has converged
# if np.max(abs(policy_evaluation(env, policy) - policy_evaluation(env, new_policy))) < theta*1e2:
# break;
policy = copy.copy(new_policy)
return policy, V
# Truncated policy evaluation
# https://github.com/xadahiya/frozen-lake-dp-rl/blob/master/Dynamic_Programming_Solution.ipynb
def truncated_policy_evaluation(env, policy, V, max_it=1, gamma=1):
num_it=0
while num_it < max_it:
for s in range(env.nS):
v = 0
q = q_from_v(env, V, s, gamma)
for a, action_prob in enumerate(policy[s]):
v += action_prob * q[a]
V[s] = v
num_it += 1
return V
# Truncated policy iteration
# https://github.com/xadahiya/frozen-lake-dp-rl/blob/master/Dynamic_Programming_Solution.ipynb
def truncated_policy_iteration(env, max_it=1, gamma=1, theta=1e-8):
V = np.zeros(env.nS)
policy = np.zeros([env.nS, env.nA]) / env.nA
while True:
policy = policy_improvement(env, V)
old_V = copy.copy(V)
V = truncated_policy_evaluation(env, policy, V, max_it, gamma)
if max(abs(V-old_V)) < theta:
break;
return policy, V
# Value iteration
# https://github.com/xadahiya/frozen-lake-dp-rl/blob/master/Dynamic_Programming_Solution.ipynb
def value_iteration(env, gamma=1, theta=1e-8):
V = np.zeros(env.nS)
while True:
delta = 0
for s in range(env.nS):
v = V[s]
V[s] = max(q_from_v(env, V, s, gamma))
delta = max(delta,abs(V[s]-v))
if delta < theta:
break
policy = policy_improvement(env, V, gamma)
return policy, V
# Get an action (0:Left, 1:Down, 2:Right, 3:Up)
def get_action(model, state):
return np.random.choice(range(4), p=model[state])
# Save a model
def save_model(bundle:(), type:str):
with open('models\\frozen_lake' + type + '.adp', 'wb') as fp:
pickle.dump(bundle, fp)
# Load a model
def load_model(type:str) -> ():
if(os.path.isfile('models\\frozen_lake' + type + '.adp') == True):
with open ('models\\frozen_lake' + type + '.adp', 'rb') as fp:
return pickle.load(fp)
else:
return (None, None)
# The main entry point for this module
def main():
# Create an environment
env = gym.make('FrozenLake8x8-v0', is_slippery=True)
# Print information about the problem
print('--- Frozen Lake ---')
print('Observation space: {0}'.format(env.observation_space))
print('Action space: {0}'.format(env.action_space))
print()
# Print one-step dynamics (probability, next_state, reward, done)
print('--- One-step dynamics')
print(env.P[1][0])
print()
# (1) Random policy
#model, V = load_model('1')
model = np.ones([env.nS, env.nA]) / env.nA
V = policy_evaluation(env, model)
print('Optimal Policy (LEFT = 0, DOWN = 1, RIGHT = 2, UP = 3):')
print(model,'\n')
plot_values(V)
save_model((model, V), '1')
# (2) Policy iteration
##model, V = load_model('2')
#model, V = policy_iteration(env)
#print('Optimal Policy (LEFT = 0, DOWN = 1, RIGHT = 2, UP = 3):')
#print(model,'\n')
#plot_values(V)
#save_model((model, V), '2')
# (3) Truncated policy iteration
##model, V = load_model('3')
#model, V = truncated_policy_iteration(env, max_it=2)
#print('Optimal Policy (LEFT = 0, DOWN = 1, RIGHT = 2, UP = 3):')
#print(model,'\n')
#plot_values(V)
#save_model((model, V), '3')
# (4) Value iteration
##model, V = load_model('4')
#model, V = value_iteration(env)
#print('Optimal Policy (LEFT = 0, DOWN = 1, RIGHT = 2, UP = 3):')
#print(model,'\n')
#plot_values(V)
#save_model((model, V), '4')
# Variables
episodes = 10
timesteps = 200
total_score = 0
# Loop episodes
for episode in range(episodes):
# Start episode and get initial observation
state = env.reset()
# Reset score
score = 0
# Loop timesteps
for t in range(timesteps):
# Get an action (0:Left, 1:Down, 2:Right, 3:Up)
action = get_action(model, state)
# Perform a step
# Observation (position, reward: 0/1, done: True/False, info: Probability)
state, reward, done, info = env.step(action)
# Update score
score += reward
total_score += reward
# Check if we are done (game over)
if done:
# Render the map
print('--- Episode {} ---'.format(episode+1))
env.render(mode='human')
print('Score: {0}, Timesteps: {1}'.format(score, t+1))
print()
break
# Close the environment
env.close()
# Print the score
print('--- Evaluation ---')
print ('Score: {0} / {1}'.format(total_score, episodes))
print()
# Tell python to run main method
if __name__ == "__main__": main()Slumpmässig policy
--- Frozen Lake ---
Observation space: Discrete(64)
Action space: Discrete(4)
--- One-step dynamics
[(0.3333333333333333, 1, 0.0, False), (0.3333333333333333, 0, 0.0, False), (0.3333333333333333, 9, 0.0, False)]
Optimal Policy (LEFT = 0, DOWN = 1, RIGHT = 2, UP = 3):
[[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]]
--- Episode 1 ---
(Down)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 0.0, Timesteps: 10
--- Episode 2 ---
(Down)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 0.0, Timesteps: 75
--- Episode 3 ---
(Up)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 0.0, Timesteps: 28
--- Episode 4 ---
(Right)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 0.0, Timesteps: 20
--- Episode 5 ---
(Down)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 0.0, Timesteps: 8
--- Episode 6 ---
(Left)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 0.0, Timesteps: 51
--- Episode 7 ---
(Up)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 0.0, Timesteps: 19
--- Episode 8 ---
(Down)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 0.0, Timesteps: 26
--- Episode 9 ---
(Left)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 0.0, Timesteps: 24
--- Episode 10 ---
(Down)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 0.0, Timesteps: 31
--- Evaluation ---
Score: 0.0 / 10Policy-iteration
--- Frozen Lake ---
Observation space: Discrete(64)
Action space: Discrete(4)
--- One-step dynamics
[(0.3333333333333333, 1, 0.0, False), (0.3333333333333333, 0, 0.0, False), (0.3333333333333333, 9, 0.0, False)]
Optimal Policy (LEFT = 0, DOWN = 1, RIGHT = 2, UP = 3):
[[0. 0.5 0.5 0. ]
[0. 0. 1. 0. ]
[0. 0. 1. 0. ]
[0. 0. 1. 0. ]
[0. 0. 1. 0. ]
[0. 0. 1. 0. ]
[0. 0. 1. 0. ]
[0. 0. 1. 0. ]
[0. 0. 0. 1. ]
[0. 0. 0. 1. ]
[0. 0. 0. 1. ]
[0. 0. 0. 1. ]
[0. 0. 0. 1. ]
[0. 0. 0. 1. ]
[0. 0. 0. 1. ]
[0. 0. 1. 0. ]
[1. 0. 0. 0. ]
[1. 0. 0. 0. ]
[1. 0. 0. 0. ]
[0.25 0.25 0.25 0.25]
[0. 0. 1. 0. ]
[0. 0. 0. 1. ]
[0. 0. 0. 1. ]
[0. 0. 1. 0. ]
[1. 0. 0. 0. ]
[1. 0. 0. 0. ]
[1. 0. 0. 0. ]
[0. 0.5 0. 0.5 ]
[1. 0. 0. 0. ]
[0.25 0.25 0.25 0.25]
[0. 0. 1. 0. ]
[0. 0. 1. 0. ]
[1. 0. 0. 0. ]
[0. 0. 0. 1. ]
[0.5 0. 0. 0.5 ]
[0.25 0.25 0.25 0.25]
[0. 0. 1. 0. ]
[0. 1. 0. 0. ]
[0. 0. 0. 1. ]
[0. 0. 1. 0. ]
[1. 0. 0. 0. ]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0. 0.5 0.5 0. ]
[0. 0. 0. 1. ]
[1. 0. 0. 0. ]
[0.25 0.25 0.25 0.25]
[0. 0. 1. 0. ]
[1. 0. 0. 0. ]
[0.25 0.25 0.25 0.25]
[0. 0.5 0.5 0. ]
[0.5 0. 0. 0.5 ]
[0.25 0.25 0.25 0.25]
[0.5 0. 0.5 0. ]
[0.25 0.25 0.25 0.25]
[0. 0. 1. 0. ]
[1. 0. 0. 0. ]
[0. 1. 0. 0. ]
[1. 0. 0. 0. ]
[0.25 0.25 0.25 0.25]
[0. 0.5 0.5 0. ]
[0. 0. 1. 0. ]
[0. 1. 0. 0. ]
[0.25 0.25 0.25 0.25]]
--- Episode 1 ---
(Right)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 1.0, Timesteps: 36
--- Episode 2 ---
(Right)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 1.0, Timesteps: 169
--- Episode 3 ---
(Right)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 1.0, Timesteps: 113
--- Episode 4 ---
(Right)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 1.0, Timesteps: 94
--- Episode 5 ---
(Right)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 1.0, Timesteps: 66
--- Episode 6 ---
(Right)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 1.0, Timesteps: 111
--- Episode 7 ---
(Right)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 1.0, Timesteps: 132
--- Episode 8 ---
(Right)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 1.0, Timesteps: 40
--- Episode 9 ---
(Right)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 1.0, Timesteps: 111
--- Episode 10 ---
(Right)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 1.0, Timesteps: 116
--- Evaluation ---
Score: 10.0 / 10Trunkerad-policy-iteration
--- Frozen Lake ---
Observation space: Discrete(64)
Action space: Discrete(4)
--- One-step dynamics
[(0.3333333333333333, 1, 0.0, False), (0.3333333333333333, 0, 0.0, False), (0.3333333333333333, 9, 0.0, False)]
Optimal Policy (LEFT = 0, DOWN = 1, RIGHT = 2, UP = 3):
[[0. 0. 1. 0. ]
[0. 0. 1. 0. ]
[0. 0. 1. 0. ]
[0. 0. 1. 0. ]
[0. 0. 1. 0. ]
[0. 0. 1. 0. ]
[0. 0. 1. 0. ]
[0. 0. 1. 0. ]
[0. 0. 0. 1. ]
[0. 0. 0. 1. ]
[0. 0. 0. 1. ]
[0. 0. 0. 1. ]
[0. 0. 0. 1. ]
[0. 0. 0. 1. ]
[0. 0. 0. 1. ]
[0. 0. 1. 0. ]
[1. 0. 0. 0. ]
[1. 0. 0. 0. ]
[1. 0. 0. 0. ]
[0.25 0.25 0.25 0.25]
[0. 0. 1. 0. ]
[0. 0. 0. 1. ]
[0. 0. 0. 1. ]
[0. 0. 1. 0. ]
[1. 0. 0. 0. ]
[1. 0. 0. 0. ]
[1. 0. 0. 0. ]
[0. 0.5 0. 0.5 ]
[1. 0. 0. 0. ]
[0.25 0.25 0.25 0.25]
[0. 0. 1. 0. ]
[0. 0. 1. 0. ]
[1. 0. 0. 0. ]
[0. 0. 0. 1. ]
[0.5 0. 0. 0.5 ]
[0.25 0.25 0.25 0.25]
[0. 0. 1. 0. ]
[0. 1. 0. 0. ]
[0. 0. 0. 1. ]
[0. 0. 1. 0. ]
[1. 0. 0. 0. ]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0. 0.5 0.5 0. ]
[0. 0. 0. 1. ]
[1. 0. 0. 0. ]
[0.25 0.25 0.25 0.25]
[0. 0. 1. 0. ]
[1. 0. 0. 0. ]
[0.25 0.25 0.25 0.25]
[0. 0.5 0.5 0. ]
[0.5 0. 0. 0.5 ]
[0.25 0.25 0.25 0.25]
[0.5 0. 0.5 0. ]
[0.25 0.25 0.25 0.25]
[0. 0. 1. 0. ]
[1. 0. 0. 0. ]
[0. 1. 0. 0. ]
[1. 0. 0. 0. ]
[0.25 0.25 0.25 0.25]
[0. 0.5 0.5 0. ]
[0. 0. 1. 0. ]
[0. 1. 0. 0. ]
[0.25 0.25 0.25 0.25]]
--- Episode 1 ---
(Right)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 1.0, Timesteps: 52
--- Episode 2 ---
(Right)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 1.0, Timesteps: 97
--- Episode 3 ---
(Right)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 1.0, Timesteps: 127
--- Episode 4 ---
(Right)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 1.0, Timesteps: 113
--- Episode 5 ---
(Right)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 1.0, Timesteps: 44
--- Episode 6 ---
(Right)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 1.0, Timesteps: 166
--- Episode 7 ---
(Right)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 1.0, Timesteps: 42
--- Episode 8 ---
(Right)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 1.0, Timesteps: 170
--- Episode 9 ---
(Right)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 1.0, Timesteps: 75
--- Episode 10 ---
(Right)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 1.0, Timesteps: 57
--- Evaluation ---
Score: 10.0 / 10Värdeiteration
--- Frozen Lake ---
Observation space: Discrete(64)
Action space: Discrete(4)
--- One-step dynamics
[(0.3333333333333333, 1, 0.0, False), (0.3333333333333333, 0, 0.0, False), (0.3333333333333333, 9, 0.0, False)]
Optimal Policy (LEFT = 0, DOWN = 1, RIGHT = 2, UP = 3):
[[0. 1. 0. 0. ]
[0. 0. 1. 0. ]
[0. 0. 1. 0. ]
[0. 0. 1. 0. ]
[0. 0. 1. 0. ]
[0. 0. 1. 0. ]
[0. 0. 1. 0. ]
[0. 0. 1. 0. ]
[0. 0. 0. 1. ]
[0. 0. 0. 1. ]
[0. 0. 0. 1. ]
[0. 0. 0. 1. ]
[0. 0. 0. 1. ]
[0. 0. 0. 1. ]
[0. 0. 0. 1. ]
[0. 0. 1. 0. ]
[1. 0. 0. 0. ]
[1. 0. 0. 0. ]
[1. 0. 0. 0. ]
[0.25 0.25 0.25 0.25]
[0. 0. 1. 0. ]
[0. 0. 0. 1. ]
[0. 0. 0. 1. ]
[0. 0. 1. 0. ]
[1. 0. 0. 0. ]
[1. 0. 0. 0. ]
[1. 0. 0. 0. ]
[0. 0.5 0. 0.5 ]
[1. 0. 0. 0. ]
[0.25 0.25 0.25 0.25]
[0. 0. 1. 0. ]
[0. 0. 1. 0. ]
[1. 0. 0. 0. ]
[0. 0. 0. 1. ]
[0.5 0. 0. 0.5 ]
[0.25 0.25 0.25 0.25]
[0. 0. 1. 0. ]
[0. 1. 0. 0. ]
[0. 0. 0. 1. ]
[0. 0. 1. 0. ]
[1. 0. 0. 0. ]
[0.25 0.25 0.25 0.25]
[0.25 0.25 0.25 0.25]
[0. 0.5 0.5 0. ]
[0. 0. 0. 1. ]
[1. 0. 0. 0. ]
[0.25 0.25 0.25 0.25]
[0. 0. 1. 0. ]
[1. 0. 0. 0. ]
[0.25 0.25 0.25 0.25]
[0. 0.5 0.5 0. ]
[0.5 0. 0. 0.5 ]
[0.25 0.25 0.25 0.25]
[0.5 0. 0.5 0. ]
[0.25 0.25 0.25 0.25]
[0. 0. 1. 0. ]
[1. 0. 0. 0. ]
[0. 1. 0. 0. ]
[1. 0. 0. 0. ]
[0.25 0.25 0.25 0.25]
[0. 0.5 0.5 0. ]
[0. 0. 1. 0. ]
[0. 1. 0. 0. ]
[0.25 0.25 0.25 0.25]]
--- Episode 1 ---
(Right)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 1.0, Timesteps: 96
--- Episode 2 ---
(Right)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 1.0, Timesteps: 116
--- Episode 3 ---
(Right)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 1.0, Timesteps: 188
--- Episode 4 ---
(Right)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 1.0, Timesteps: 124
--- Episode 5 ---
(Right)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 0.0, Timesteps: 200
--- Episode 6 ---
(Right)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 1.0, Timesteps: 71
--- Episode 7 ---
(Right)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 1.0, Timesteps: 90
--- Episode 8 ---
(Right)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 1.0, Timesteps: 102
--- Episode 9 ---
(Right)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 1.0, Timesteps: 52
--- Episode 10 ---
(Right)
SFFFFFFF
FFFFFFFF
FFFHFFFF
FFFFFHFF
FFFHFFFF
FHHFFFHF
FHFFHFHF
FFFHFFFG
Score: 0.0, Timesteps: 200
--- Evaluation ---
Score: 8.0 / 10