Heltalsprogrammering i Python

Jag kommer att lösa ett problem med hjälp av heltalsprogrammering i denna handledning. Heltalsprogrammering (IP) är en optimeringsmetod som är begränsad till att använda heltalsvariabler, variabler med binära värden (0 och 1) är vanliga i IP-problem. Heltalsprogrammering är en form av linjär programmering som kan användas när variabler representerar beslut, när vi vill veta om vi ska ta vissa beslut eller inte (Ja/Nej).

IP används för schemaläggning, tilldelning och beslutsfattande. Heltalsprogrammering antar att ett problem kan representeras som en matematisk modell med linjära relationer. Ett IP-problem representeras av en målfunktion, variabler som kan modifieras och begränsningar. Jag använder Python och pulp-biblioteket i den här handledningen.

Kapitalbudgetering

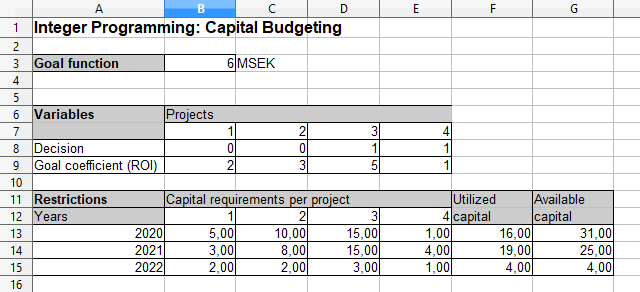
Ett företag har identifierat fyra olika projekt som möjliga investeringar, företaget har uppskattat potentiell avkastning för varje projekt och kapitalkraven för varje projekt. Varje projekt tar tre år att slutföra, men företaget har inte en obegränsad mängd kapital att investera. Målet är att maximera den totala avkastningen på investeringarna med hänsyn tagen till kapitalbegränsningar.

Jag har skapat och löst problemet i OpenOffice Calc. Den bästa lösningen är att genomföra projekt 3 och 4, detta ger en total avkastning om 6 MSEK.

Kod

Koden nedan visar en implementering av heltalsprogrammering för att lösa ett kapitalbudgeteringsproblem. Problemet formuleras och får sin lösning med hjälp av pulp, resultatet från en körning visas nedanför koden.

# Import libraries
import pulp

# The main entry point for this module
def main():
    
    # Create a problem
    # Either LpMinimize (default) or LpMaximize
    problem = pulp.LpProblem('Capital-Budgeting', pulp.LpMaximize)

    # Projects
    projects = ['1', '2', '3', '4']

    # Return on investments (MSEK)
    roi = {'1':2, '2':3, '3':5, '4':1}

    # Capital requirments (MSEK)
    y2020 = {'1':5, '2':10, '3':15, '4':1}
    y2021 = {'1':3, '2':8, '3':15, '4':4}
    y2022 = {'1':2, '2':2, '3':3, '4':1}

    # Create decision variables (values that can be modified by solver)
    # Category: Integer, Binary or Continuous(default)
    decision = pulp.LpVariable.dicts('Project', projects, lowBound=None, upBound=None, cat='Binary')

    # Objective function
    problem += pulp.lpSum([roi[i] * decision[i] for i in projects])

    # Constraints
    problem += pulp.lpSum([y2020[i] * decision[i] for i in projects]) <= 31
    problem += pulp.lpSum([y2021[i] * decision[i] for i in projects]) <= 25
    problem += pulp.lpSum([y2022[i] * decision[i] for i in projects]) <= 4
    
    # Print problem
    print(problem)

    # Write problem data to an .lp file
    problem.writeLP('plots\\capital_budgeting.lp')

    # Solve the problem by using PuLP's choice of Solver
    problem.solve()

    # Print the status of the solution
    print('Status: {0}\n'.format(pulp.LpStatus[problem.status]))

    # Print each variable with optimal value
    print('Decisions')
    for v in problem.variables():
        print(v.name, "=", v.varValue)
    print()

    # Print the optimal goal value
    print('Total Return On Investments (MSEK) = {0}\n'.format(pulp.value(problem.objective)))

# Tell python to run main method
if __name__ == '__main__': main()

Resultat

Capital-Budgeting:
MAXIMIZE
2*Project_1 + 3*Project_2 + 5*Project_3 + 1*Project_4 + 0
SUBJECT TO
_C1: 5 Project_1 + 10 Project_2 + 15 Project_3 + Project_4 <= 31

_C2: 3 Project_1 + 8 Project_2 + 15 Project_3 + 4 Project_4 <= 25

_C3: 2 Project_1 + 2 Project_2 + 3 Project_3 + Project_4 <= 4

VARIABLES
0 <= Project_1 <= 1 Integer
0 <= Project_2 <= 1 Integer
0 <= Project_3 <= 1 Integer
0 <= Project_4 <= 1 Integer

Status: Optimal

Decisions
Project_1 = 0.0
Project_2 = 0.0
Project_3 = 1.0
Project_4 = 1.0

Total Return On Investments (MSEK) = 6.0