Linjär programmering i Python

Jag kommer att lösa ett problem med hjälp av linjär programmering i denna handledning. Linjär programmering (LP) är en optimeringsteknik som används för att hitta den bästa lösningen på ett problem genom att maximera eller minimera en mål-funktion med hänsyn tagen till begränsningar. LP används vanligtvis vid planering, för att uppnå det bästa resultatet med hänsyn tagen till restriktioner.

LP används i matematik, företagsekonomi, nationalekonomi och teknik, metoden används för planering, dirigering, schemaläggning, tilldelning och design. Linjär programmering antar att ett problem kan representeras som en matematisk modell med linjära relationer. Ett LP-problem representeras med en mål-funktion, variabler som kan modifieras och begränsningar. Jag använder Python och pulp-biblioteket i den här handledningen.

Produktionsplanering

Ett företag tillverkar stolar, bord och pallar. Genom licensavtal har företaget också fått möjlighet att tillverka högst 1 200 hyllor per månad. Torkning av målade möbler är en trång sektion, man kan bara måla och torka ett visst antal stolar, bord, pallar och hyllor per månad. Målet är att hitta den optimala produktmixen att tillverka under varje månad.

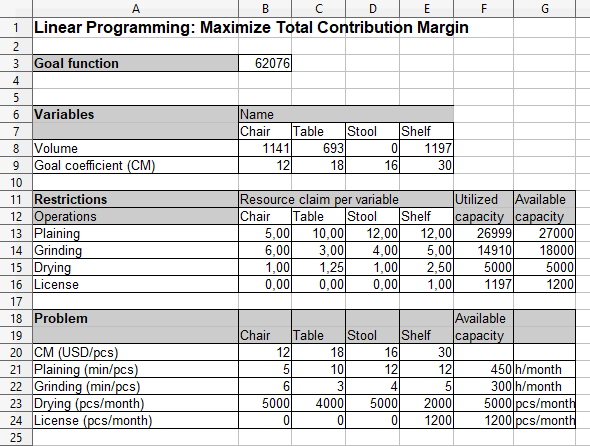
Jag har strukturerat och löst problemet i OpenOffice Calc. Fabriken har tre operationer (hyvling, slipning and torkning) och en licensbegränsning. Jag har standardiserat resursanspråket för torkning, detta för att få en normaliserad resursbegränsning för alla produkter. Målfunktionen är att maximera det totala täckningsbidraget (TCM), summan av volymer multiplicerat med målkoefficienter.

Kod

Koden nedan visar en implementering av linjär programmering för att lösa ett produktionsplaneringsproblem. Problemet formuleras och får sin lösning med hjälp av pulp, resultatet från en körning visas under koden.

# Import libraries
import pulp

# The main entry point for this module
def main():
    
    # Create a problem
    # Either LpMinimize (default) or LpMaximize
    problem = pulp.LpProblem('Maximize-TCM', pulp.LpMaximize)

    # Products
    products = ['Chair', 'Table', 'Stool', 'Shelf']

    # Contribution margins
    cm = {'Chair':12, 'Table':18, 'Stool':16, 'Shelf':30}

    # Resource consumption
    plaining = {'Chair':5, 'Table':10, 'Stool':12, 'Shelf':12}
    grinding = {'Chair':6, 'Table':3, 'Stool':4, 'Shelf':5}
    drying = {'Chair':1, 'Table':1.25, 'Stool':1, 'Shelf':2.5}
    license = {'Chair':0, 'Table':0, 'Stool':0, 'Shelf':1}

    # Create decision variables (values that can be modified by solver)
    # Category: Integer, Binary or Continuous(default)
    volume = pulp.LpVariable.dicts('Volume', products, lowBound=0, upBound=None, cat='Integer')

    # Objective function
    problem += pulp.lpSum([cm[i] * volume[i] for i in products])

    # Constraints
    problem += pulp.lpSum([plaining[i] * volume[i] for i in products]) <= 27000
    problem += pulp.lpSum([grinding[i] * volume[i] for i in products]) <= 18000
    problem += pulp.lpSum([drying[i] * volume[i] for i in products]) <= 5000
    problem += pulp.lpSum([license[i] * volume[i] for i in products]) <= 1200

    # Print problem
    print(problem)

    # Write problem data to an .lp file
    problem.writeLP('plots\\production.lp')

    # Solve the problem by using PuLP's choice of Solver
    problem.solve()

    # Print the status of the solution
    print('Status: {0}\n'.format(pulp.LpStatus[problem.status]))

    # Print each variable with optimal value
    print('Volumes')
    for v in problem.variables():
        print(v.name, "=", v.varValue)
    print()

    # Print the optimal goal value
    print('Total Contribution Margin (TCM) = {0}\n'.format(pulp.value(problem.objective)))

# Tell python to run main method
if __name__ == '__main__': main()

Resultat

Maximize-TCM:
MAXIMIZE
12*Volume_Chair + 30*Volume_Shelf + 16*Volume_Stool + 18*Volume_Table + 0
SUBJECT TO
_C1: 5 Volume_Chair + 12 Volume_Shelf + 12 Volume_Stool + 10 Volume_Table
 <= 27000

_C2: 6 Volume_Chair + 5 Volume_Shelf + 4 Volume_Stool + 3 Volume_Table
 <= 18000

_C3: Volume_Chair + 2.5 Volume_Shelf + Volume_Stool + 1.25 Volume_Table
 <= 5000

_C4: Volume_Shelf <= 1200

VARIABLES
0 <= Volume_Chair Integer
0 <= Volume_Shelf Integer
0 <= Volume_Stool Integer
0 <= Volume_Table Integer

Status: Optimal

Volumes
Volume_Chair = 1132.0
Volume_Shelf = 1200.0
Volume_Stool = 0.0
Volume_Table = 694.0

Total Contribution Margin (TCM) = 62076.0