Denna handledning visar hur du implementerar en linjär regressionsalgoritm för att förutsäga aktiekurser i Python. Jag använder data från Ericsson AB för att förutsäga Ericssons aktiekurs. Jag ska förbereda data, visualisera data, träna en modell, utvärdera modellen och använda modellen för att göra förutsägelser.
Aktiekurser återspeglar förväntningar om förmågan att generera kassaflöden och resultat i framtiden. Resultatet är mer stabilt än kassaflödet, men resultatet påverkas av tillämpade redovisningsstandarder. Min teori är att aktiekurserna påverkas av intäkter, resultat, eget kapital, fritt kassaflöde, förändringar i intäkter, förändringar i resultat, förändringar i fritt kassaflöde och räntesatsen. Räntan är ett alternativ till investeringar i aktier och påverkar avkastningskravet. Jag kommer att använda marknadsvärde (aktiekurs * antal aktier) som målvärde, detta för att göra modellen oberoende av antalet aktier.
Aktiekurser påverkas av utdelningar, en aktiekurs sjunker vanligtvis med ett belopp som motsvarar utdelningen per aktie på utbetalningsdagen. Jag har justerat fria kassaflöden för nyemissioner och utdelningar. Resultatet har inte justerats för utdelning men eget kapital påverkas av lämnade utdelningar då eget kapital minskar när det har skett en utdelning.
Aktiekurser påverkas främst av förväntningar om framtiden och jag kommer att ta hänsyn till detta genom att använda årliga intäkter, årligt resultat och årligt fritt kassaflöde från årets första dag. Min indata kommer att ha dagliga förändringar i marknadsvärde och ränta men endast årliga förändringar i intäkter, resultat, fritt kassaflöde, eget kapital, intäktsökning, vinsttillväxt och tillväxt i fria kassaflöden. Tillväxt mäts som skillnaden mellan intäkter, resultat eller fria kassaflöden under ett år jämfört med föregående år. Det är omöjligt att använda procentuella förändringar eftersom resultaten kan vara både negativa och positiva.
Aktiekurser rör sig upp och ner i ett kort perspektiv, men de tenderar att röra sig mot ett genomsnittspris över tid (återgång till medelvärdet). En linjär regressionsmodell handlar om medelvärden eftersom regression innebär att värden kommer att återgå till medelvärdet. Linjär regression modellerar ett samband mellan en beroende variabel (Y) och en eller flera oberoende variabler (X). En linjär regressionsmodell vill hitta den funktion som bäst passar indata.
Datauppsättning och bibliotek
Jag kommer att använda en datauppsättning (ladda ner) med information om Ericsson AB i denna handledning. Ericsson AB grundades 1918 och har haft perioder med hög tillväxt, perioder med stagnation och perioder med minskande tillväxt. Denna datamängd innehåller data från 1987 till 2018, den har en beroende variabel (marknadsvärde) och 8 oberoende variabler. Du behöver följande bibliotek för den här handledningen: numpy, pandas, matplotlib, statsmodels, scikit-learn och joblib.
Gemensam modul
Jag har en gemensam modul (common.py) som innehåller en metod. Mappstrukturen för den här modulen är annytab/stock_prediction och det betyder att namnområdet är annytab.stock_prediction. Alla andra moduler lagras i samma mapp.
# Remove outliers from a data set
def remove_outliers(ds, col_name):
q1 = ds[col_name].quantile(0.25)
q3 = ds[col_name].quantile(0.75)
iqr = q3-q1 #Interquartile range
fence_low = q1-1.5*iqr
fence_high = q3+1.5*iqr
ds = ds.loc[(ds[col_name] > fence_low) & (ds[col_name] < fence_high)]
return dsFörbered data
Vi har en modul som är avsedd för dataförberedelse och datavisualisering. Innehållet i denna fil visas nedan.
# Import libraries
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.api as sm
import annytab.stock_prediction.common as common
# Visualize the dataset
def visualize(ds):
# Count the number columns
count = len(ds.columns.values)
# Print number of columns
print('--- Columns ---\n')
print(count)
# Get data labels (all labels except the target label)
data_labels = list(ds.columns.values[1:count])
ols_labels = data_labels.copy()
ols_labels.insert(0, 'CONSTANT')
# Print first 5 rows in data set
print('\n--- First 5 rows ---\n')
print(ds.head())
# Print the shape
print('\n--- Shape of data set ---\n')
print(ds.shape)
# Print labels
print('\n--- Data labels ---\n')
print(data_labels)
# Plot Y in a line diagram
figure = plt.figure(figsize = (12, 8))
figure.suptitle('ERICSSON B', fontsize=16)
plt.plot(ds['MARKET VALUE'])
plt.ylabel('MARKET VALUE')
plt.xlabel('INDICES')
#plt.show() # Show or save the plot (can not do both)
plt.savefig('plots\\ericsson-chart.png')
plt.close()
# Scatter plots (8 subplots in 1 figure)
figure = plt.figure(figsize = (12, 8))
figure.suptitle('CORRELATION WITH MARKET VALUE', fontsize=16)
plt.subplots_adjust(top = 0.9, bottom=0.1, hspace=0.5, wspace=0.2)
for i, value in enumerate(data_labels):
plt.subplot(2, 4, i + 1) # 2 rows and 4 columns
plt.scatter(ds[value], ds['MARKET VALUE'])
plt.title(value)
#plt.show() # Show or save the plot (can not do both)
plt.savefig('plots\\ericsson-scatterplots.png')
plt.close()
# Slice data set in data (X) and target (Y)
X = dataset.values[:,1:count] # DATA
Y = dataset.values[:,0] # MARKET VALUE
# Output OLS-statistics
X = sm.add_constant(X)
model = sm.OLS(Y, X)
model.data.ynames = 'MARKET VALUE'
model.data.xnames = ols_labels
results = model.fit()
f = open('plots\\ericsson-summary.txt', 'w')
f.write(str(results.summary()))
f.close()
# Load data set
dataset = pd.read_csv('files\\ericsson.csv', sep=';')
# Remove outliers
#dataset = common.remove_outliers(dataset, 'MARKET VALUE')
# Remove E-CHANGE and FCF-CHANGE
#dataset = dataset.drop(columns=['E-CHANGE', 'FCF-CHANGE'])
# Visualize data set
visualize(dataset)Läs in datauppsättning och visualisera data
Datauppsättningen laddas in med pandas genom att använda en relativ sökväg till projektets rot, använd en absolut sökväg om dina filer lagras utanför projektet. Vi kommer att skriva ut information om datauppsättningen och skapa diagram för att lära oss mer om datauppsättningen.
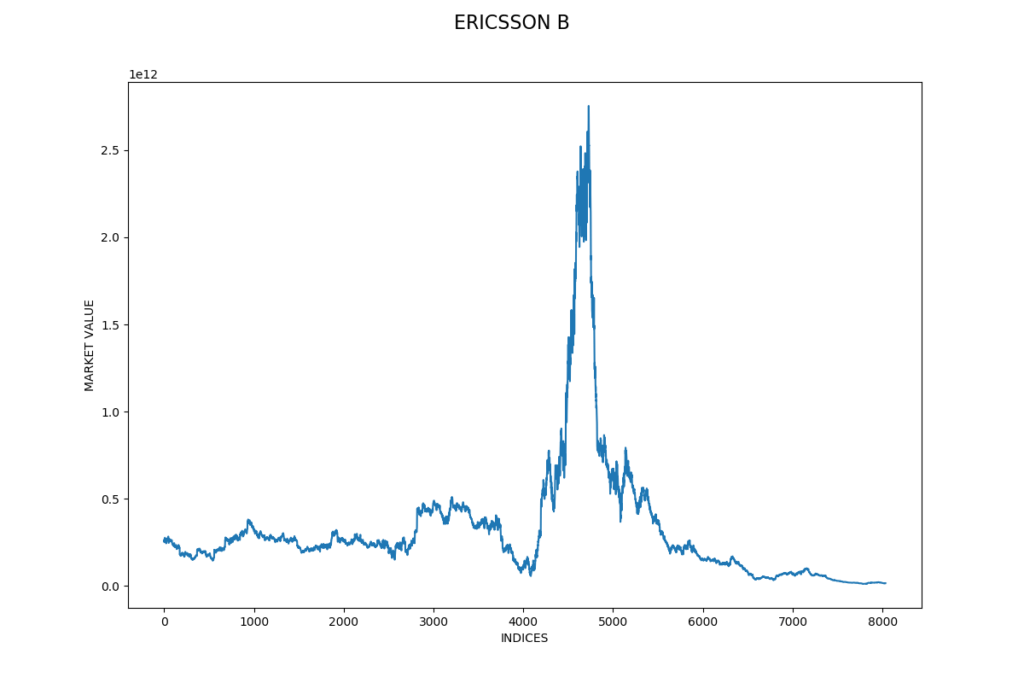
Marknadsvärdet beräknas som aktiekursen multiplicerat med det totala antalet aktier i slutet av år 2018. Ericssons aktiekurs hade en stark ökning och ett stort fall under perioden mellan slutet av år 1999 och början av år 2001. Detta var under it-bubblan, det var en period med överdriven spekulation och många teknikföretag hade övervärderade aktiekurser. Vi kan behöva ta bort extremvärden i vår datauppsättning för att kunna få bättre förutsägelser.
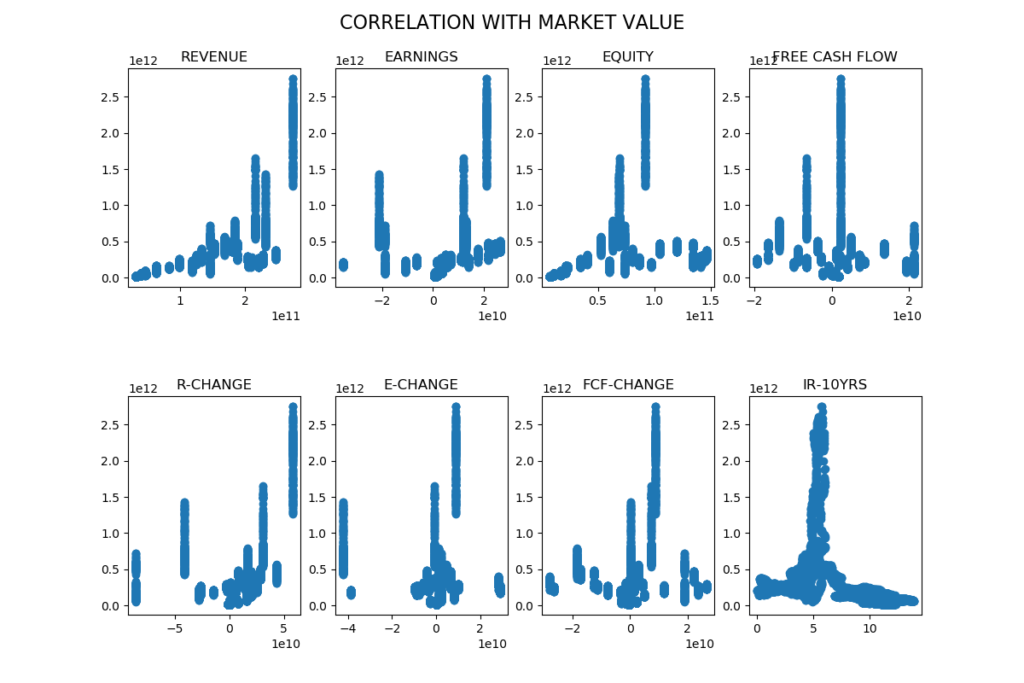
Varje oberoende variabel har plottats mot marknadsvärdet, detta för att få en visuell bild av sambandet mellan varje oberoende variabel och marknadsvärdet. Korrelationen verkar vara bäst mellan intäkter och marknadsvärde.
OLS Regression Results
==============================================================================
Dep. Variable: MARKET VALUE R-squared: 0.709
Model: OLS Adj. R-squared: 0.709
Method: Least Squares F-statistic: 2446.
Date: Mon, 25 Nov 2019 Prob (F-statistic): 0.00
Time: 10:29:00 Log-Likelihood: -2.2056e+05
No. Observations: 8035 AIC: 4.411e+05
Df Residuals: 8026 BIC: 4.412e+05
Df Model: 8
Covariance Type: nonrobust
==================================================================================
coef std err t P>|t| [0.025 0.975]
----------------------------------------------------------------------------------
CONSTANT -6.663e+11 2.32e+10 -28.669 0.000 -7.12e+11 -6.21e+11
REVENUE 8.9168 0.078 113.885 0.000 8.763 9.070
EARNINGS 13.1772 0.380 34.645 0.000 12.432 13.923
EQUITY -8.3278 0.142 -58.667 0.000 -8.606 -8.050
FREE CASH FLOW 1.9080 0.424 4.502 0.000 1.077 2.739
R-CHANGE -1.9292 0.148 -13.025 0.000 -2.220 -1.639
E-CHANGE -0.4610 0.253 -1.825 0.068 -0.956 0.034
FCF-CHANGE -0.0176 0.275 -0.064 0.949 -0.556 0.521
IR-10YRS 3.67e+10 1.85e+09 19.861 0.000 3.31e+10 4.03e+10
==============================================================================
Omnibus: 3545.022 Durbin-Watson: 0.012
Prob(Omnibus): 0.000 Jarque-Bera (JB): 25831.027
Skew: 1.966 Prob(JB): 0.00
Kurtosis: 10.855 Cond. No. 2.03e+12
==============================================================================
Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
[2] The condition number is large, 2.03e+12. This might indicate that there are
strong multicollinearity or other numerical problems.Jag har använt en OLS-modell från statsmodels för att få en statistisk sammanfattning av en linjär regression. Förklaringsgraden (r-kvadrat) är 70,9% och F-värdet är 2446, detta betyder att modellen är signifikant. E-CHANGE och FCF-CHANGE är inte signifikanta i ett t-test, sannolikheten för att få ett högre t-värde är för hög. Jag har beslutat att ta bort E-CHANGE och FCF-CHANGE från datauppsättningen, jag kommer också att ta bort extremvärden i datauppsättningen.
Träning och utvärdering
Datauppsättningen läses in och delas upp i data (X) och målvärde (Y). Datauppsättningen delas upp i en träningsuppsättning och en testuppsättning enligt ett 80/20-förhållande, 80 % för träning och 20 % för test. Jag har utfört en rutnätsökning och använder informationen från den här processen för att sätta parametrar i modellen.
# Import libraries
import numpy as np
import pandas as pd
import sklearn
import sklearn.linear_model
import sklearn.metrics
import sklearn.pipeline
import joblib
import matplotlib.pyplot as plt
import annytab.stock_prediction.common as common
# Variables
number_of_shares = 3334151735
# Perform a grid search to find the best parameters
def grid_search(X, Y):
# Create a pipeline
clf_pipeline = sklearn.pipeline.Pipeline([
('m', sklearn.linear_model.LinearRegression(copy_X=True, n_jobs=2))
])
# Set parameters (name in pipeline + name of parameter)
parameters = {
'm__fit_intercept': (True, False),
'm__normalize': (True, False)
}
# Create a grid search classifier
#print(sklearn.metrics.SCORERS.keys())
gs_classifier = sklearn.model_selection.GridSearchCV(clf_pipeline, parameters, cv=10, iid=False, n_jobs=2, scoring='neg_mean_squared_error', verbose=1)
# Start a search (Warning: can take a long time if the whole dataset is used)
gs_classifier = gs_classifier.fit(X, Y)
# Print results
print('---- Results ----')
print('Best score: ' + str(gs_classifier.best_score_))
for name in sorted(parameters.keys()):
print('{0}: {1}'.format(name, gs_classifier.best_params_[name]))
# Train and evaluate
def train_and_evaluate(X, Y):
# Create a model
model = sklearn.linear_model.LinearRegression(copy_X=True, fit_intercept=True, normalize=False, n_jobs=2)
# Train the model
model.fit(X, Y)
# Save the model (Make sure that the folder exists)
joblib.dump(model, 'models\\linear_regression.jbl')
# Evaluate on training data
print('\n-- Training data --\n')
predictions = model.predict(X)
print('r2 (coefficient of determination): {0:.2f}'.format(sklearn.metrics.r2_score(Y, predictions)))
print('RMSE: {0:.2f}'.format(np.sqrt(sklearn.metrics.mean_squared_error(Y, predictions))))
print('')
# Evaluate with 10-fold CV
print('\n-- 10-fold CV --\n')
predictions = sklearn.model_selection.cross_val_predict(model, X, Y, cv=10)
print('r2 (coefficient of determination): {0:.2f}'.format(sklearn.metrics.r2_score(Y, predictions)))
print('RMSE: {0:.2f}'.format(np.sqrt(sklearn.metrics.mean_squared_error(Y, predictions))))
# Test and evaluate
def test_and_evaluate(X, Y):
# Load the model
model = joblib.load('models\\linear_regression.jbl')
# Make predictions
predictions = model.predict(X)
# Print results
print('\n---- Results ----')
for i in range(len(predictions)):
print('Predicted: {0:.2f}, Actual: {1:.2f}'.format(predictions[i] / number_of_shares, Y[i] / number_of_shares))
print('r2 (coefficient of determination): {0:.2f}'.format(sklearn.metrics.r2_score(Y, predictions)))
rmse = np.sqrt(sklearn.metrics.mean_squared_error(Y, predictions))
print('RMSE: {0:.2f}'.format(rmse))
print('RMSE / share: {0:.2f}'.format(rmse / number_of_shares))
# Make predictions
def predict(X):
# Load the model
model = joblib.load('models\\linear_regression.jbl')
# Make predictions
predictions = model.predict(X)
# Print results
print('\n---- Results ----')
for i in range(len(predictions)):
print('Input: {0}, Predicted: {1:.2f}'.format(X[i], predictions[i] / number_of_shares))
# Plot predictions
prices = predictions / number_of_shares
figure = plt.figure(figsize = (12, 8))
figure.suptitle('FUTURE PRICE PREDICTIONS', fontsize=16)
plt.plot(prices + 1.96 * 25.74, color='red')
plt.plot(prices - 1.96 * 25.74, color='red')
plt.plot(['2019', '2020', '2021'], prices)
plt.xlabel('Years')
plt.savefig('plots\\ericsson-predictions.png')
# The main entry point for this module
def main():
# Load data set
ds = pd.read_csv('files\\ericsson.csv', sep=';')
# Remove outliers
ds = common.remove_outliers(ds, 'MARKET VALUE')
# Remove E-CHANGE and FCF-CHANGE
ds = ds.drop(columns=['E-CHANGE', 'FCF-CHANGE'])
# Count the number columns
count = len(ds.columns.values)
# Get data labels (all labels except the target label)
data_labels = list(ds.columns.values[1:count])
# Slice data set in data (X) and target (Y)
X = ds.values[:,1:count] # DATA
Y = ds.values[:,0] # MARKET VALUE
# Split data set in train and test (use random state to get the same split every time)
X_train, X_test, Y_train, Y_test = sklearn.model_selection.train_test_split(X, Y, test_size=0.2, random_state=2)
# Perform a grid search
#grid_search(X_train, Y_train)
# Train and evaluate
train_and_evaluate(X_train, Y_train)
# Test and evaluate
#test_and_evaluate(X_test, Y_test)
# Predict on estimates [REVENUE, EARNINGS, EQUITY, FREE CASH FLOW, R-CHANGE, IR
#estimates = [[226852000000.000, 2892000000.000, 85935700952.700, -3698055738.150, 16014000000.000, 0.500],
# [236050000000.000, 16239000000.000, 96740033624.650, 11131283567.850, 9198000000.000, 0.500],
# [242666000000.000, 19144000000.000, 108715607394.400, 13377256804.450, 6616000000.000, 0.500]]
#predict(estimates)
# Tell python to run main method
if __name__ == "__main__": main()Utdata från rutnätssökning och utvärdering
Fitting 10 folds for each of 4 candidates, totalling 40 fits
[Parallel(n_jobs=2)]: Using backend LokyBackend with 2 concurrent workers.
[Parallel(n_jobs=2)]: Done 40 out of 40 | elapsed: 0.8s finished
---- Results ----
Best score: -6.932311663824655e+21
m__fit_intercept: True
m__normalize: False-- Training data --
r2 (coefficient of determination): 0.71
RMSE: 83107645234.47
-- 10-fold CV --
r2 (coefficient of determination): 0.71
RMSE: 83260504825.67Testa och utvärdera
Den tränade och sparade modellen utvärderas på testuppsättningen. Jag läser in den sparade modellen och utvärderar modellen på förklaringsgrad och standardavvikelse. Marknadsvärdet divideras med det totala antalet aktier i slutet av år 2018.
Predicted: 111.80, Actual: 113.10
Predicted: 21.13, Actual: 20.18
Predicted: 17.38, Actual: 4.52
Predicted: 95.71, Actual: 75.90
Predicted: 35.90, Actual: 38.53
Predicted: 142.09, Actual: 133.97
Predicted: 69.47, Actual: 63.20
Predicted: 80.97, Actual: 59.65
Predicted: 121.41, Actual: 113.98
Predicted: 68.39, Actual: 85.55
Predicted: 20.06, Actual: 8.59
Predicted: 19.87, Actual: 10.07
Predicted: 22.12, Actual: 63.60
Predicted: 68.54, Actual: 69.80
Predicted: 64.61, Actual: 74.00
Predicted: 22.69, Actual: 19.16
Predicted: 33.87, Actual: 35.61
Predicted: 111.21, Actual: 86.75
Predicted: 83.96, Actual: 104.50
Predicted: 172.00, Actual: 201.32
Predicted: 101.12, Actual: 137.50
Predicted: 101.50, Actual: 138.50
Predicted: 96.09, Actual: 128.75
Predicted: 101.50, Actual: 137.50
Predicted: 100.67, Actual: 127.00
Predicted: 21.30, Actual: 18.83
Predicted: 108.88, Actual: 75.90
Predicted: 63.56, Actual: 87.90
Predicted: 122.36, Actual: 142.41
Predicted: 17.37, Actual: 17.97
Predicted: 21.32, Actual: 19.76
Predicted: 17.29, Actual: 6.80
Predicted: 105.57, Actual: 82.10
Predicted: 101.36, Actual: 134.50
Predicted: 106.22, Actual: 87.10
Predicted: 158.11, Actual: 193.19
Predicted: 67.68, Actual: 75.70
Predicted: 122.78, Actual: 132.48
Predicted: 16.24, Actual: 5.02
Predicted: 21.71, Actual: 52.50
Predicted: 62.98, Actual: 80.95
Predicted: 107.23, Actual: 55.88
Predicted: 21.97, Actual: 25.24
Predicted: 95.76, Actual: 127.20
Predicted: 22.80, Actual: 29.44
Predicted: 18.07, Actual: 7.79
Predicted: 83.37, Actual: 102.00
Predicted: 17.77, Actual: 7.36
Predicted: 17.30, Actual: 6.30
Predicted: 171.55, Actual: 206.74
Predicted: 105.74, Actual: 79.05
Predicted: 109.13, Actual: 81.80
Predicted: 63.88, Actual: 67.71
Predicted: 86.49, Actual: 92.31
Predicted: 96.22, Actual: 129.50
Predicted: 68.31, Actual: 79.70
Predicted: 21.86, Actual: 57.55
Predicted: 107.58, Actual: 63.42
Predicted: 68.25, Actual: 67.00
Predicted: 16.67, Actual: 4.52
Predicted: 107.52, Actual: 63.50
Predicted: 17.08, Actual: 3.61
Predicted: 142.70, Actual: 189.58
Predicted: 67.74, Actual: 71.30
Predicted: 84.90, Actual: 82.50
Predicted: 157.94, Actual: 189.13
Predicted: 21.91, Actual: 47.39
Predicted: 33.19, Actual: 67.50
Predicted: 65.13, Actual: 68.15
Predicted: 64.12, Actual: 59.81
Predicted: 34.29, Actual: 44.25
Predicted: 32.51, Actual: 20.67
Predicted: 96.03, Actual: 122.90
Predicted: 55.83, Actual: 38.21
Predicted: 111.41, Actual: 91.05
Predicted: 22.37, Actual: 23.27
Predicted: 21.79, Actual: 23.38
Predicted: 21.89, Actual: 52.75
Predicted: 122.36, Actual: 163.18
Predicted: 63.38, Actual: 63.65
Predicted: 106.59, Actual: 62.60
Predicted: 23.37, Actual: 20.46
Predicted: 20.37, Actual: 8.57
Predicted: 81.25, Actual: 61.70
Predicted: 95.82, Actual: 95.00
Predicted: 84.67, Actual: 65.90
Predicted: 121.30, Actual: 111.94
Predicted: 111.30, Actual: 82.45
Predicted: 80.75, Actual: 59.75
Predicted: 105.92, Actual: 81.20
Predicted: 158.21, Actual: 177.85
Predicted: 81.00, Actual: 62.50
Predicted: 108.80, Actual: 75.35
Predicted: 68.38, Actual: 86.40
Predicted: 158.22, Actual: 150.76
Predicted: 63.84, Actual: 166.83
Predicted: 21.83, Actual: 49.45
Predicted: 24.60, Actual: 11.69
Predicted: 21.79, Actual: 13.31
Predicted: 20.67, Actual: 13.96
Predicted: 71.37, Actual: 68.80
Predicted: 20.58, Actual: 8.31
Predicted: 21.71, Actual: 56.55
Predicted: 64.42, Actual: 40.25
Predicted: 81.07, Actual: 63.50
Predicted: 101.27, Actual: 134.75
Predicted: 19.72, Actual: 17.14
Predicted: 70.95, Actual: 81.60
Predicted: 50.12, Actual: 43.62
Predicted: 105.98, Actual: 51.90
Predicted: 64.06, Actual: 36.50
Predicted: 96.07, Actual: 134.50
Predicted: 84.18, Actual: 133.50
Predicted: 65.15, Actual: 69.65
Predicted: 96.49, Actual: 126.25
Predicted: 158.00, Actual: 208.99
Predicted: 22.61, Actual: 29.42
Predicted: 33.27, Actual: 59.50
Predicted: 83.26, Actual: 106.00
Predicted: 21.90, Actual: 23.49
Predicted: 85.22, Actual: 61.39
Predicted: 80.92, Actual: 59.10
Predicted: 71.23, Actual: 70.90
Predicted: 65.29, Actual: 65.80
Predicted: 107.33, Actual: 54.30
Predicted: 24.75, Actual: 12.12
Predicted: 80.62, Actual: 65.90
Predicted: 107.78, Actual: 73.10
Predicted: 84.37, Actual: 67.48
Predicted: 107.72, Actual: 67.78
Predicted: 64.24, Actual: 29.75
Predicted: 141.71, Actual: 184.17
Predicted: 68.66, Actual: 74.25
Predicted: 20.77, Actual: 12.88
Predicted: 64.02, Actual: 193.19
Predicted: 111.33, Actual: 95.50
Predicted: 63.71, Actual: 165.75
Predicted: 100.91, Actual: 118.50
Predicted: 111.98, Actual: 110.60
Predicted: 33.74, Actual: 36.25
Predicted: 19.56, Actual: 11.91
Predicted: 142.46, Actual: 196.81
Predicted: 122.29, Actual: 159.79
Predicted: 62.04, Actual: 66.46
Predicted: 22.41, Actual: 29.66
Predicted: 71.98, Actual: 54.30
Predicted: 101.33, Actual: 138.50
Predicted: 108.45, Actual: 79.50
Predicted: 16.34, Actual: 5.48
Predicted: 61.27, Actual: 66.02
Predicted: 17.12, Actual: 5.69
Predicted: 19.59, Actual: 13.07
Predicted: 35.39, Actual: 47.08
Predicted: 111.48, Actual: 78.80
Predicted: 101.01, Actual: 139.00
Predicted: 80.96, Actual: 59.85
Predicted: 105.10, Actual: 81.20
Predicted: 23.18, Actual: 20.13
Predicted: 21.81, Actual: 52.40
Predicted: 106.05, Actual: 79.50
Predicted: 68.44, Actual: 67.00
Predicted: 21.93, Actual: 26.84
Predicted: 17.11, Actual: 5.50
Predicted: 84.31, Actual: 140.00
Predicted: 157.51, Actual: 191.39
Predicted: 72.72, Actual: 48.00
Predicted: 63.20, Actual: 76.30
Predicted: 17.15, Actual: 5.30
Predicted: 64.42, Actual: 43.50
Predicted: 105.14, Actual: 79.00
Predicted: 22.55, Actual: 28.68
Predicted: 63.85, Actual: 167.92
Predicted: 34.72, Actual: 39.18
Predicted: 22.45, Actual: 19.16
Predicted: 63.47, Actual: 75.11
Predicted: 107.54, Actual: 77.06
Predicted: 16.31, Actual: 5.50
Predicted: 85.02, Actual: 105.50
Predicted: 68.66, Actual: 75.15
Predicted: 101.06, Actual: 125.25
Predicted: 73.00, Actual: 61.50
Predicted: 84.36, Actual: 131.00
Predicted: 84.94, Actual: 58.91
Predicted: 95.99, Actual: 131.20
Predicted: 105.64, Actual: 78.70
Predicted: 141.88, Actual: 129.64
Predicted: 16.69, Actual: 3.96
Predicted: 106.49, Actual: 44.00
Predicted: 83.97, Actual: 134.00
Predicted: 121.78, Actual: 123.00
Predicted: 61.12, Actual: 44.16
Predicted: 105.04, Actual: 76.80
Predicted: 21.25, Actual: 19.01
Predicted: 105.29, Actual: 81.90
Predicted: 81.01, Actual: 61.25
Predicted: 19.74, Actual: 17.47
Predicted: 111.76, Actual: 107.00
Predicted: 67.85, Actual: 79.80
Predicted: 64.05, Actual: 69.74
Predicted: 158.29, Actual: 143.09
Predicted: 17.00, Actual: 3.79
Predicted: 80.45, Actual: 68.30
Predicted: 100.82, Actual: 109.00
Predicted: 17.94, Actual: 7.58
Predicted: 141.94, Actual: 184.17
Predicted: 84.02, Actual: 136.50
Predicted: 101.01, Actual: 133.00
Predicted: 157.62, Actual: 188.68
Predicted: 65.03, Actual: 68.50
Predicted: 104.76, Actual: 77.30
Predicted: 61.19, Actual: 62.56
Predicted: 109.23, Actual: 67.15
Predicted: 32.93, Actual: 29.11
Predicted: 63.48, Actual: 69.33
Predicted: 61.17, Actual: 44.54
Predicted: 106.80, Actual: 92.70
Predicted: 106.46, Actual: 44.66
Predicted: 108.74, Actual: 79.40
Predicted: 24.23, Actual: 17.32
Predicted: 68.47, Actual: 82.60
Predicted: 84.94, Actual: 58.91
Predicted: 171.47, Actual: 209.44
Predicted: 104.97, Actual: 77.40
Predicted: 63.40, Actual: 84.86
Predicted: 95.68, Actual: 76.20
Predicted: 16.87, Actual: 3.49
Predicted: 22.20, Actual: 23.49
Predicted: 172.15, Actual: 183.72
Predicted: 80.95, Actual: 62.20
Predicted: 19.78, Actual: 9.65
Predicted: 107.79, Actual: 76.60
Predicted: 85.17, Actual: 60.71
Predicted: 101.08, Actual: 138.75
Predicted: 64.48, Actual: 18.25
Predicted: 67.63, Actual: 73.20
Predicted: 142.05, Actual: 205.83
Predicted: 106.64, Actual: 59.60
Predicted: 107.72, Actual: 70.50
Predicted: 111.40, Actual: 105.60
Predicted: 108.45, Actual: 79.80
Predicted: 35.25, Actual: 38.31
Predicted: 71.35, Actual: 67.20
Predicted: 84.27, Actual: 137.00
Predicted: 158.13, Actual: 142.64
Predicted: 67.50, Actual: 72.20
Predicted: 34.02, Actual: 27.50
Predicted: 63.67, Actual: 87.70
Predicted: 85.41, Actual: 118.00
Predicted: 111.53, Actual: 82.15
Predicted: 81.10, Actual: 64.30
Predicted: 158.40, Actual: 165.66
Predicted: 80.12, Actual: 68.15
Predicted: 85.45, Actual: 68.84
Predicted: 33.82, Actual: 54.50
Predicted: 19.91, Actual: 9.22
Predicted: 35.70, Actual: 49.46
Predicted: 19.90, Actual: 16.84
Predicted: 158.11, Actual: 139.93
Predicted: 106.14, Actual: 89.65
Predicted: 60.55, Actual: 51.47
Predicted: 63.46, Actual: 93.89
Predicted: 68.44, Actual: 69.40
Predicted: 63.02, Actual: 78.90
Predicted: 22.04, Actual: 60.65
Predicted: 111.26, Actual: 93.80
Predicted: 34.25, Actual: 34.85
Predicted: 108.39, Actual: 84.45
Predicted: 109.02, Actual: 82.20
Predicted: 100.74, Actual: 107.50
Predicted: 17.46, Actual: 4.44
Predicted: 65.44, Actual: 66.55
Predicted: 33.95, Actual: 44.00
Predicted: 107.48, Actual: 81.70
Predicted: 157.67, Actual: 188.91
Predicted: 95.89, Actual: 73.85
Predicted: 34.21, Actual: 35.93
Predicted: 63.47, Actual: 166.83
Predicted: 158.34, Actual: 153.47
Predicted: 64.37, Actual: 42.00
Predicted: 83.30, Actual: 106.00
Predicted: 54.23, Actual: 39.29
Predicted: 21.45, Actual: 13.10
Predicted: 95.62, Actual: 132.80
Predicted: 34.03, Actual: 23.20
Predicted: 63.30, Actual: 85.22
Predicted: 68.51, Actual: 81.70
Predicted: 101.00, Actual: 133.50
Predicted: 63.31, Actual: 75.98
Predicted: 33.83, Actual: 35.75
Predicted: 21.13, Actual: 20.89
Predicted: 63.92, Actual: 43.33
Predicted: 67.97, Actual: 68.50
Predicted: 63.31, Actual: 138.67
Predicted: 122.22, Actual: 110.82
Predicted: 65.23, Actual: 67.75
Predicted: 21.88, Actual: 60.85
r2 (coefficient of determination): 0.70
RMSE: 85811896806.55
RMSE / share: 25.74Förutsägelser baserade på uppskattningar
Jag har samlat in uppskattningar för Ericsson från MarketScreener och använder dessa uppskattningar för att göra förutsägelser avseende åren 2019, 2020 och 2021. Marknadsvärdet divideras med det totala antalet aktier i slutet av år 2018. Resultatet från denna förutsägelse visas nedan.
---- Results ----
Input: [226852000000.0, 2892000000.0, 85935700952.7, -3698055738.15, 16014000000.0, 0.5], Predicted: 149.83
Input: [236050000000.0, 16239000000.0, 96740033624.65, 11131283567.85, 9198000000.0, 0.5], Predicted: 183.77
Input: [242666000000.0, 19144000000.0, 108715607394.4, 13377256804.45, 6616000000.0, 0.5], Predicted: 184.23