Jag kommer att implementera en SVM-algoritm (Support Vector Machine) för klassificering i denna handledning. Jag kommer att visualisera datauppsättningen, hitta de bästa hyperparametrarna att använda, träna en modell och utvärdera resultaten. Support Vector Machine är en snabb algoritm som kan användas för att klassificera datauppsättningar med linjär separation, SVM:s kan vara hjälpfulla vid textkategorisering.
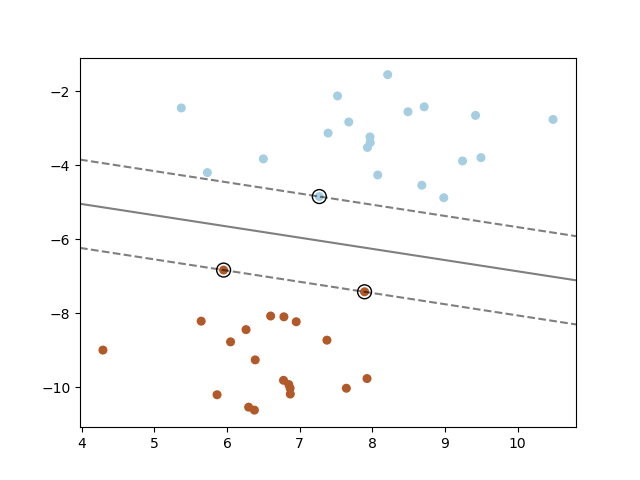
Support Vector Machine kan användas för binära klassificeringsproblem och för flerklassproblem. Support Vector Machine är en linjär metod och fungerar därför inte bra för datauppsättningar som har en icke-linjär struktur. Support Vector Machine kan användas med icke-linjär data om man tillämpar kärntricket. Support Vector Machine försöker konstruera centrerade hyperplan mellan klasser, algoritmen vill hitta hyperplan som har den högsta marginalen mellan grupper av datapunkter. Datapunkterna närmast hyperplanet kallas supportvektorer.
Support Vector Machine-algoritmen är enkel att använda, den är snabb och den resulterande modellen tar inte mycket hårddiskutrymme i anspråk. Scikit-learn har tre modeller för SVM som skiljer sig åt i implementeringen: SVC, NuSVC och LinearSVC. SVC är baserad på libsvm, passningstiden skalas åtminstone kvadratiskt med antalet datapunkter. NuSVC, liknar SVC men använder en parameter för att kontrollera antalet supportvektorer. LinearSVC liknar SVC, men den använder en linjär kärna och implementeras i termer av liblinear snarare än libsvm. Jag kommer att använda LinearSVC eftersom den skalar bäst till ett stora datauppsättningar.
Datauppsättning och bibliotek
Jag kommer att använda datauppsättningen Iris (ladda ner) i den här handledningen. Iris-uppsättningen består av 150 blommor, varje blomma har fyra indatavärden och ett målvärde. Jag använder också följande bibliotek: pandas, joblib, numpy, matplotlib och scikit-learn.
Python-modul
Jag har inkluderat all kod i en fil, ett projekt består normalt av många filer (moduler). Du kan skapa namnområden genom att placera filer i mappar och du importerar en fil med dess namnområden plus dess filnamn. En fil med namnet common.py i mappen annytab/learning importeras som import annytab.learn.common. Jag kommer att förklara mer om koden i avsnitten nedan.
# Import libraries
import pandas
import joblib
import numpy as np
import matplotlib.pyplot as plt
import sklearn.model_selection
import sklearn.svm
import sklearn.metrics
import sklearn.pipeline
# Visualize data set
def visualize_dataset(ds):
# Print first 5 rows in data set
print('--- First 5 rows ---\n')
print(ds.head())
# Print the shape
print('\n--- Shape of data set ---\n')
print(ds.shape)
# Print class distribution
print('\n--- Class distribution ---\n')
print(ds.groupby('species').size())
# Box plots
plt.figure(figsize = (12, 8))
ds.boxplot()
#plt.show()
plt.savefig('plots\\iris-boxplots.png')
plt.close()
# Scatter plots (4 subplots in 1 figure)
figure = plt.figure(figsize = (12, 8))
grouped_dataset = ds.groupby('species')
values = ['sepal_length', 'sepal_width', 'petal_length', 'petal_width']
for i, value in enumerate(values):
plt.subplot(2, 2, i + 1) # 2 rows and 2 columns
for name, group in grouped_dataset:
plt.scatter(group.index, ds[value][group.index], label=name)
plt.ylabel(value)
plt.xlabel('index')
plt.legend()
#plt.show()
plt.savefig('plots\\iris-scatterplots.png')
# Train and evaluate
def train_and_evaluate(X, Y):
# Create a model
model = sklearn.svm.LinearSVC(penalty='l1', loss='squared_hinge', dual=False, tol=0.0001, C=0.4, multi_class='ovr',
fit_intercept=True, intercept_scaling=1, class_weight=None, verbose=0, random_state=None, max_iter=10000)
# Train the model on the whole data set
model.fit(X, Y)
# Save the model (Make sure that the folder exists)
joblib.dump(model, 'models\\svm.jbl')
# Evaluate on training data
print('\n-- Training data --\n')
predictions = model.predict(X)
accuracy = sklearn.metrics.accuracy_score(Y, predictions)
print('Accuracy: {0:.2f}'.format(accuracy * 100.0))
print('Classification Report:')
print(sklearn.metrics.classification_report(Y, predictions))
print('Confusion Matrix:')
print(sklearn.metrics.confusion_matrix(Y, predictions))
print('')
# Evaluate with 10-fold CV
print('\n-- 10-fold CV --\n')
predictions = sklearn.model_selection.cross_val_predict(model, X, Y, cv=10)
accuracy = sklearn.metrics.accuracy_score(Y, predictions)
print('Accuracy: {0:.2f}'.format(accuracy * 100.0))
print('Classification Report:')
print(sklearn.metrics.classification_report(Y, predictions))
print('Confusion Matrix:')
print(sklearn.metrics.confusion_matrix(Y, predictions))
# Perform a grid search to find the best hyperparameters
def grid_search(X, Y):
# Create a pipeline
clf_pipeline = sklearn.pipeline.Pipeline([
('m', sklearn.svm.LinearSVC(loss='squared_hinge', tol=0.0001, multi_class='ovr', dual=False, class_weight=None, verbose=0, random_state=None, max_iter=10000))
])
# Set parameters (name in pipeline + name of parameter)
parameters = {
'm__penalty': ('l1', 'l2'),
'm__C': (0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0),
'm__fit_intercept': (False, True),
'm__intercept_scaling': (0.5, 1, 2)
}
# Create a grid search classifier
gs_classifier = sklearn.model_selection.GridSearchCV(clf_pipeline, parameters, cv=10, iid=False, n_jobs=2, scoring='accuracy', verbose=1)
# Start a search (Warning: can take a long time if the whole dataset is used)
gs_classifier = gs_classifier.fit(X, Y)
# Print results
print('---- Results ----')
print('Best score: ' + str(gs_classifier.best_score_))
for name in sorted(parameters.keys()):
print('{0}: {1}'.format(name, gs_classifier.best_params_[name]))
# Predict and evaluate on test data
def predict_and_evaluate(X, Y):
# Load the model
model = joblib.load('models\\svm.jbl')
# Make predictions
predictions = model.predict(X)
# Print results
print('\n---- Results ----')
for i in range(len(predictions)):
print('Input: {0}, Predicted: {1}, Actual: {2}'.format(X[i], predictions[i], Y[i]))
accuracy = sklearn.metrics.accuracy_score(Y, predictions)
print('\nAccuracy: {0:.2f}'.format(accuracy * 100.0))
print('\nClassification Report:')
print(sklearn.metrics.classification_report(Y, predictions))
print('Confusion Matrix:')
print(sklearn.metrics.confusion_matrix(Y, predictions))
# The main entry point for this module
def main():
# Load data set (includes header values)
dataset = pandas.read_csv('files\\iris.csv')
# Visualize data set
visualize_dataset(dataset)
# Slice data set in values and targets (2D-array)
X = dataset.values[:,0:4]
Y = dataset.values[:,4]
# Split data set in train and test (use random state to get the same split every time, and stratify to keep balance)
X_train, X_test, Y_train, Y_test = sklearn.model_selection.train_test_split(X, Y, test_size=0.2, random_state=1, stratify=Y)
# Make sure that data still is balanced
print('\n--- Class balance ---\n')
print(np.unique(Y_train, return_counts=True))
print(np.unique(Y_test, return_counts=True))
# Perform a grid search
#grid_search(X, Y)
# Train and evaluate
#train_and_evaluate(X_train, Y_train)
# Predict on test set
predict_and_evaluate(X_test, Y_test)
# Tell python to run main method
if __name__ == "__main__": main()Läs in och visualisera datauppsättningen
Datauppsättningen laddas med pandas genom att använda en relativ sökväg, använd en absolut sökväg om dina filer lagras utanför projektet. Vi vill visualisera datauppsättningen för att se till att den är balanserad och vi vill lära oss mer om datauppsättningen. Det är viktigt att ha en balanserad datauppsättning vid klassificering, varje klass tränas lika frekvent med en balanserad träningsuppsättning. Vi kan plotta en datauppsättning för att hitta mönster, ta bort extremvärden och för att besluta om de lämpligaste algoritmerna att använda.
# Load data set (includes header values)
dataset = pandas.read_csv('files\\iris.csv')
# Visualize data set
visualize_dataset(dataset)
--- First 5 rows ---
sepal_length sepal_width petal_length petal_width species
0 5.1 3.5 1.4 0.2 Iris-setosa
1 4.9 3.0 1.4 0.2 Iris-setosa
2 4.7 3.2 1.3 0.2 Iris-setosa
3 4.6 3.1 1.5 0.2 Iris-setosa
4 5.0 3.6 1.4 0.2 Iris-setosa
--- Shape of dataset ---
(150, 5)
--- Class distribution ---
species
Iris-setosa 50
Iris-versicolor 50
Iris-virginica 50
dtype: int64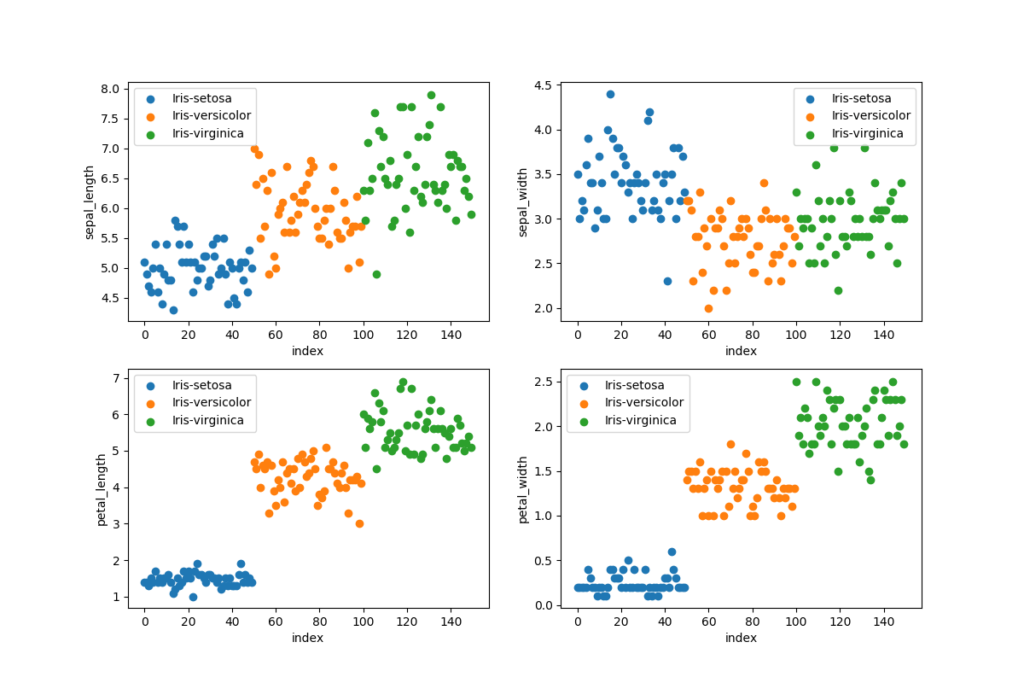
Dela upp datauppsättningen
Jag måste först dela upp värden i datauppsättningen för att få indata (X) och utdata (Y), de första 4 kolumnerna är indata och den sista kolumnen utgör målvärdet. Jag delar upp datauppsättningen i en träningsuppsättning och en testuppsättning, 80 % är för träning och 20 % för test. Jag vill se till att datauppsättningarna fortfarande är balanserade efter denna delning och jag använder därför en stratify-parameter.
# Slice data set in values and targets (2D-array)
X = dataset.values[:,0:4]
Y = dataset.values[:,4]
# Split data set in train and test (use random state to get the same split every time, and stratify to keep balance)
X_train, X_test, Y_train, Y_test = sklearn.model_selection.train_test_split(X, Y, test_size=0.2, random_state=1, stratify=Y)
# Make sure that data still is balanced
print('\n--- Class balance ---\n')
print(np.unique(Y_train, return_counts=True))
print(np.unique(Y_test, return_counts=True))Baslinjeprestanda
Vår datauppsättning har 150 blommor och 50 blommor i varje klass, vår träningsuppsättning har samma balans. En slumpvis förutsägelse kommer att vara korrekt i 33% (50/150) av alla fall och vår modell måste ha en noggrannhet som är bättre än 33 % för att vara användbar.
Rutnätssökning
Jag gör en rutnätsökning för att hitta de bästa parametrarna för träning. En rutnätsökning kan ta lång tid att utföra på stora datauppsättningar, men det är antagligen snabbare jämfört med en manuell process. Resultatet från denna process visas nedan och jag kommer att använda dessa parametrar när jag tränar modellen.
# Perform a grid search
grid_search(X, Y)
Fitting 10 folds for each of 108 candidates, totalling 1080 fits
[Parallel(n_jobs=2)]: Using backend LokyBackend with 2 concurrent workers.
[Parallel(n_jobs=2)]: Done 968 tasks | elapsed: 2.9s
[Parallel(n_jobs=2)]: Done 1080 out of 1080 | elapsed: 3.1s finished
---- Results ----
Best score: 0.9666666666666668
m__C: 0.4
m__fit_intercept: True
m__intercept_scaling: 1
m__penalty: l1Träning och utvärdering
Jag tränar modellen genom att använda parametrarna från rutnätsökningen och sparar modellen till en fil med joblib. Utvärderingen görs på träningsuppsättningen och med korsvalidering. Korsvalideringsutvärderingen ger en antydan om modellens generaliseringsprestanda. Jag hade 95 % exakthet på träningsdata och 95 % exakthet med tiofaldig korsvalidering.
# Train and evaluate
train_and_evaluate(X_train, Y_train)
-- Training data --
Accuracy: 95.00
Classification Report:
precision recall f1-score support
Iris-setosa 1.00 1.00 1.00 40
Iris-versicolor 0.95 0.90 0.92 40
Iris-virginica 0.90 0.95 0.93 40
accuracy 0.95 120
macro avg 0.95 0.95 0.95 120
weighted avg 0.95 0.95 0.95 120
Confusion Matrix:
[[40 0 0]
[ 0 36 4]
[ 0 2 38]]
-- 10-fold CV --
Accuracy: 95.00
Classification Report:
precision recall f1-score support
Iris-setosa 1.00 1.00 1.00 40
Iris-versicolor 0.93 0.93 0.93 40
Iris-virginica 0.93 0.93 0.93 40
accuracy 0.95 120
macro avg 0.95 0.95 0.95 120
weighted avg 0.95 0.95 0.95 120
Confusion Matrix:
[[40 0 0]
[ 0 37 3]
[ 0 3 37]]Test och utvärdering
Det sista steget i denna process är att göra förutsägelser och utvärdera prestationer avseende testdata. Jag läser in modellen, gör förutsägelser och skriver ut resultaten. X-variabeln är en 2D-array, om du vill göra en förutsägelse för en blomma måste du ange indata så här: X = np.array ([[7.3, 2.9, 6.3, 1.8]]).
# Predict on test set
predict_and_evaluate(X_test, Y_test)
---- Results ----
Input: [7.3 2.9 6.3 1.8], Predicted: Iris-virginica, Actual: Iris-virginica
Input: [4.9 3.1 1.5 0.1], Predicted: Iris-setosa, Actual: Iris-setosa
Input: [5.1 2.5 3.0 1.1], Predicted: Iris-versicolor, Actual: Iris-versicolor
Input: [4.8 3.4 1.6 0.2], Predicted: Iris-setosa, Actual: Iris-setosa
Input: [5.0 3.5 1.6 0.6], Predicted: Iris-setosa, Actual: Iris-setosa
Input: [5.1 3.5 1.4 0.2], Predicted: Iris-setosa, Actual: Iris-setosa
Input: [6.2 3.4 5.4 2.3], Predicted: Iris-virginica, Actual: Iris-virginica
Input: [6.4 2.7 5.3 1.9], Predicted: Iris-virginica, Actual: Iris-virginica
Input: [5.6 2.8 4.9 2.0], Predicted: Iris-virginica, Actual: Iris-virginica
Input: [6.8 2.8 4.8 1.4], Predicted: Iris-versicolor, Actual: Iris-versicolor
Input: [5.4 3.9 1.3 0.4], Predicted: Iris-setosa, Actual: Iris-setosa
Input: [5.5 2.3 4.0 1.3], Predicted: Iris-versicolor, Actual: Iris-versicolor
Input: [6.8 3.0 5.5 2.1], Predicted: Iris-virginica, Actual: Iris-virginica
Input: [6.0 2.2 4.0 1.0], Predicted: Iris-versicolor, Actual: Iris-versicolor
Input: [5.7 2.5 5.0 2.0], Predicted: Iris-virginica, Actual: Iris-virginica
Input: [5.7 4.4 1.5 0.4], Predicted: Iris-setosa, Actual: Iris-setosa
Input: [7.1 3.0 5.9 2.1], Predicted: Iris-virginica, Actual: Iris-virginica
Input: [6.1 2.8 4.0 1.3], Predicted: Iris-versicolor, Actual: Iris-versicolor
Input: [4.9 2.4 3.3 1.0], Predicted: Iris-versicolor, Actual: Iris-versicolor
Input: [6.1 3.0 4.9 1.8], Predicted: Iris-virginica, Actual: Iris-virginica
Input: [6.4 2.9 4.3 1.3], Predicted: Iris-versicolor, Actual: Iris-versicolor
Input: [5.6 3.0 4.5 1.5], Predicted: Iris-versicolor, Actual: Iris-versicolor
Input: [4.9 3.1 1.5 0.1], Predicted: Iris-setosa, Actual: Iris-setosa
Input: [4.4 2.9 1.4 0.2], Predicted: Iris-setosa, Actual: Iris-setosa
Input: [6.5 3.0 5.2 2.0], Predicted: Iris-virginica, Actual: Iris-virginica
Input: [4.9 2.5 4.5 1.7], Predicted: Iris-virginica, Actual: Iris-virginica
Input: [5.4 3.9 1.7 0.4], Predicted: Iris-setosa, Actual: Iris-setosa
Input: [4.8 3.0 1.4 0.1], Predicted: Iris-setosa, Actual: Iris-setosa
Input: [6.3 3.3 4.7 1.6], Predicted: Iris-versicolor, Actual: Iris-versicolor
Input: [6.5 2.8 4.6 1.5], Predicted: Iris-versicolor, Actual: Iris-versicolor
Accuracy: 100.00
Classification Report:
precision recall f1-score support
Iris-setosa 1.00 1.00 1.00 10
Iris-versicolor 1.00 1.00 1.00 10
Iris-virginica 1.00 1.00 1.00 10
accuracy 1.00 30
macro avg 1.00 1.00 1.00 30
weighted avg 1.00 1.00 1.00 30
Confusion Matrix:
[[10 0 0]
[ 0 10 0]
[ 0 0 10]]